HDG methods
new HDG methods for convected waves in time-harmonic domain
Our objective is to develop efficient and reliable numerical method for aeroacoustic problems arising in computational helioseismology. As Hybridizable Discontinuous Galerkin (HDG) methods have demonstrated their efficiency for solving seismic inverse problem, we have chosen to build our computational environment on those formulations.
HDG methods are a particular class of mixed DG-methods where a new hybrid unknown, called the numerical trace is introduced. This unknown is only defined on the skeleton of the mesh and allows the elimination of the interior degrees of freedom using a static condensation process. Thank to this elimination, HDG methods are far less expensive as usual DG methods. Indeed as the main unknown of HDG lives on the skeleton of the mesh, a HDG method in dimension ( n ) is only as expensive as a DG method in dimension ( n-1 ). This is illustrated in the figure below.
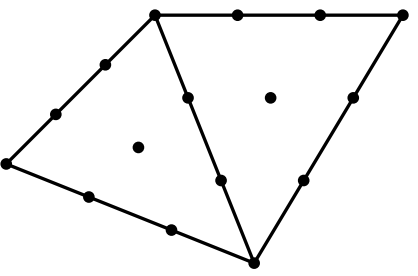
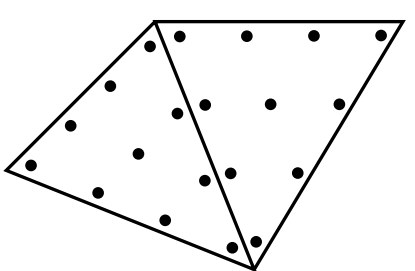
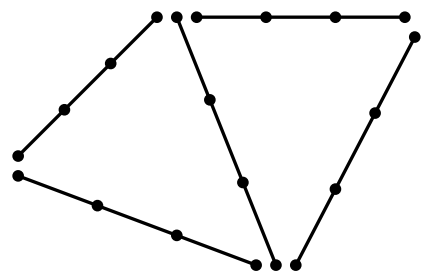
By using HDG methods we can therefore keep the advantages of the DG methods, such as
- hp-adaptivity,
- high-order,
- easy parrallelization,
for a reduced numerical cost.
It is also important to notice that HDG methods belong to the family of mixed finite-element methods. This allows the approximation of non-standard Hilbert spaces, which arise in some realistic helioseismic problems.
As a first step towards the development of HDG methods for realistic simulations in helioseismology, we have designed three variations of the HDG method for the convected Helmholtz equation. For those formulations, we provide an implementation in the open-source software hawen, as well as a detailed anlysis including the following results :
- global solvability: well-posedness of the problem involving the numerical trace only,
- local solvability: well-posedness of the local operator used to reconstruct the initial unknowns once the global problem has been solved,
- convergence rates for regular solutions,
- a discussion on the choice of penalization parameter.
Want to see how it works ?
Click here if you wish to see some math
Starting from the convected Helmholtz equation $$ -\omega^2 p-2i\omega\vec{v_0}\cdot\nabla p -\vec{v_0}\cdot\nabla[\vec{v_0}\cdot\nabla p]-\mathrm{div}\left(c_0^2\nabla p\right)=s, $$ we introduce the matrix \( M_0 = c_0^2\mathrm{Id}-\vec{v_0}\vec{v_0}^T \) and the total flux \( \vec\sigma=-M_0\nabla p -2i\omega p \vec{v_0} \) to reach the following first-order in space formulation $$ \left\{\begin{array}{cc} M_0^{-1}\vec\sigma + \nabla p + 2i\omega p M_0^{-1}\vec{v_0} &= 0, \\ -\omega^2 p +\mathrm{div}(\vec\sigma) &= s. \end{array}\right. $$ The key ingredient of HDG methods is the trace unknown \( \lambda_h\) which approximates \( p \) on the skeleton of the mesh \( \mathcal T_h \). In the variational formulation, boundary integrals involving \( p \) will be discretized by boundary integrals involving \( \lambda_h \), eg. $$ \int_{\partial K} p_h \vec r\cdot \vec n \mathrm ds \ \overset{\text{becomes}}{\longrightarrow} \ \int_{\partial K} \lambda_h \vec r\cdot\vec n\mathrm ds. $$ On an element \(K\) of the mesh, each unknown is approximated by a polynomial function : \(p^K_h\in\mathcal P(K)\) and \(\vec\sigma^K_h\in\vec{\mathcal P}(K) \), this leads to the following local prolem $$ \mathbb A^K\begin{bmatrix} p_h^K \\ \vec\sigma_h^K \end{bmatrix} + \mathbb C^K\left[\lambda_h\right]=\mathbb S^K. $$ As the approximation spaces are discontinuous, we need to glue the elements together. This is done by choosing the numerical flux between two elements for \( \vec\sigma \) as $$ \widehat{\vec\sigma}^K_h\cdot\vec n = \vec\sigma_h^K\cdot\vec n + i\omega\tau\left(p_h^K-\lambda_h\right), $$ where \( \tau \) is a penalization parameter that controls the stability of the method. This choice ensures the normal continuity of \( \vec\sigma \) on the interface between two elements. Using the approximation spaces for \( p_h^K \) and \( \vec\sigma_h^K \) in the transmission condition, we obtain $$ \sum_{K\in\mathcal T_{h}} \left( \mathbb B^K\begin{bmatrix} p_h^K \\ \vec\sigma_h^K \end{bmatrix} + \mathbb L^K\left[\lambda_h\right] \right) = 0. $$ Here \( \mathbb B^K \) and \( \mathbb L^K \) are surfacic terms. We can now eliminate the interior nodes of the local problem to obtain an expression of the local unknowns in terms of \( \lambda_h \) $$ \begin{bmatrix} p_h^K \\ \vec\sigma_h^K \end{bmatrix} = (\mathbb{A}^K)^{-1}\mathbb{S}^K-(\mathbb{A}^K)^{-1}\mathbb{C}^K\left[\lambda_h\right]. $$ Finally, by using this last formula in the transmission condition, we can obtain the global problem $$ \sum_{K\in\mathcal{T}_h}\left(\mathbb L^K-\mathbb B^K(\mathbb A^K)^{-1}\mathbb C^K\right)\left[\lambda_h\right]=-\sum_{K\in\mathcal T_h}\mathbb B^K(\mathbb A^K)^{-1}\mathbb S^K, $$ which is the main problem of the HDG method. Solving an equation using a HDG method is therefore a two-step process :- Solving the global problem for \( \lambda_h \),
- Reconstructring \( p_h^K \) and \( \vec\sigma_h^K \) on each element \( K\in\mathcal T_h \).
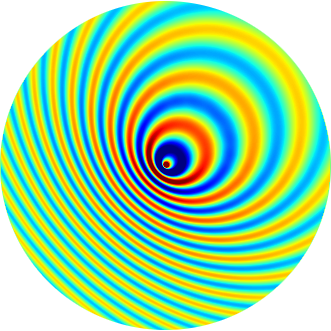
Some numerical results